二級建築士試験分野別まとめ
構造
応力度と許容応力度

2023年7月02日(日)
令和05年度試験日まであと 日!
このWEBサイトは建築士試験に限定した資料集です
(公益財団法人よりWEB上での公開認定取得済)
分野別にまとめました
(平成20年度から令和02年度まで)
二級建築士
構造
応力度と許容応力度
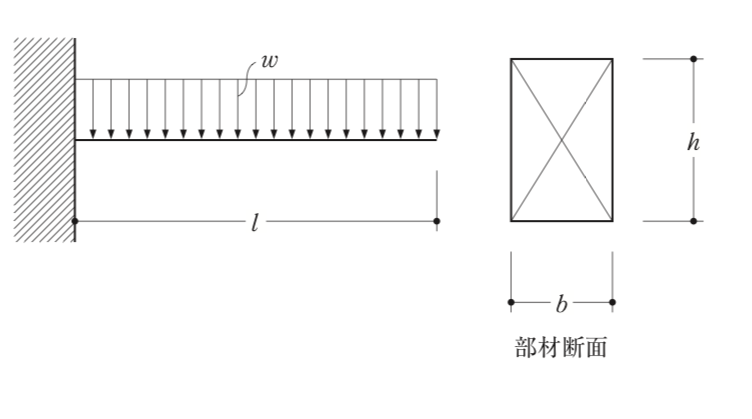
〔R02 No.2〕図のような等分布荷重wを受ける長さlの片持ち梁に断面b×hの部材を用いたとき、その部材に生じる最大曲げ応力度として、正しいものは、次のうちどれか。ただし、部材の自重は無視するものとする。
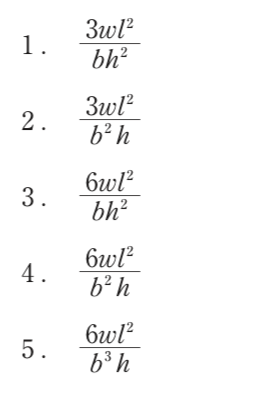
解答 1:
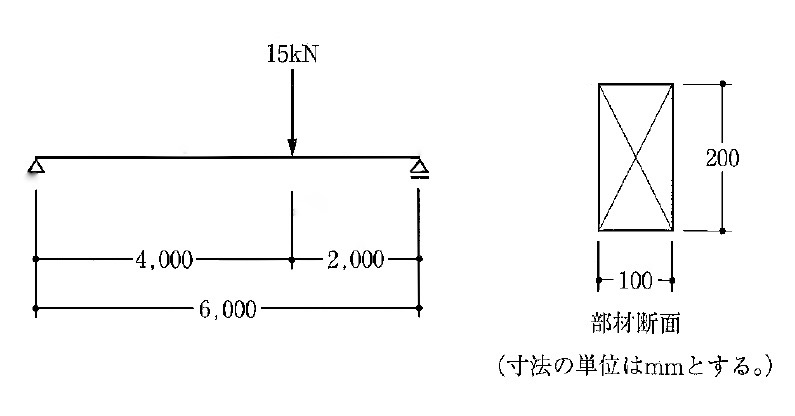
〔R01 No.2〕図のような荷重を受ける単純梁に断面100mm×200mmの部材を用いた場合、その部材に生じる最大曲げ応力度として、正しいものは、次のうちどれか。ただし、部材の自重は無視するものとする。
1.30 N/mm2
2.45 N/mm2
3.60 N/mm2
4.75 N/mm2
5.90 N/mm2
解答 1:最大曲げ応力度は、M / Z で求められる。
曲げモーメントは外力15kNが加わる点で最大になる。左支点における鉛直反力をR左とすると、
M(曲げモーメント) = R左 × 4,000 = 5 × 4,000 = 20,000 kN・mm = 20,000,000 N・mm
Z(断面係数) = bh2 / 6 = 100 × 2002 / 6 = 4,000,000 / 6 mm3
よって、最大曲げ応力度は、
M / Z = 20,000,000 × 6 / 4,000,000 = 30 N/mm2
〔H30 No.2〕図のような荷重を受ける単純梁に、断面90 mm×200 mmの部材を用いた場合、その部材が許容曲げモーメントに達するときの荷重P の値として、正しいものは、次のうちどれか。ただし、部材の許容曲げ応力度は20 N/mm2とし、自重は無視するものとする。
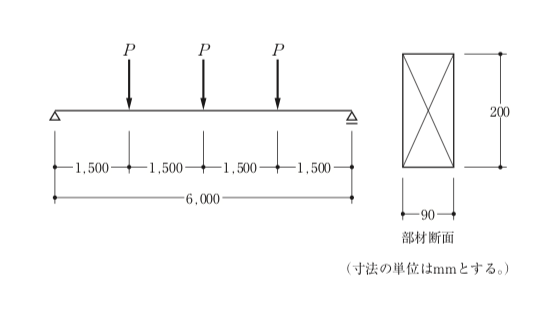
1.2 kN
2.4 kN
3.6 kN
4.8 kN
5.12 kN
解答 2:
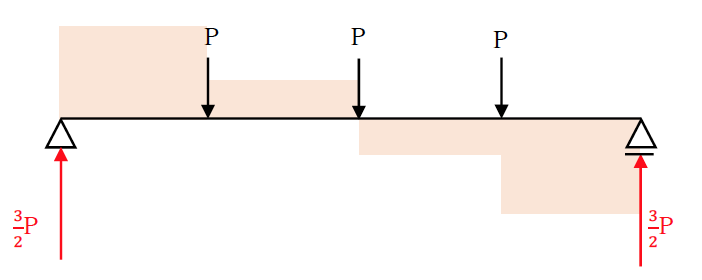
最大曲げモーメントを求め、許容モーメントに達する時の荷重Pを求める。
最大曲げモーメントMmaxは、上図のQ図より、
Mmax=1.5PN×1,500mm+0.5PN+1,500mm=3,000PN•mm
許容曲げモーメントMaは、
Ma=Z×fb
=(bh2/12)×fb
=(90mm×(200mm)2/12)×20N/mm2
=600,000mm3×20N/mm2=12,000,000N•mm
Mmax=Maとなるので、
3,000PN•mm=12,000,000N•mm
P=4,000N=4kN
〔H29 No.2〕図のような等分布荷重を受ける単純梁に断面100mm×200mmの部材を用いた場合、A点に生じる最大曲げ応力度として、正しいものは、次のうちどれか。ただし、部材の断面は一様とし、自重は無視するものとする。
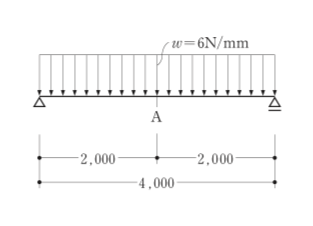
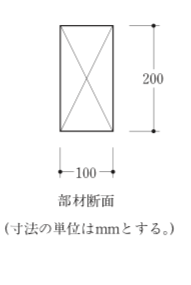
1.6 N/mm2
2.9 N/mm2
3.12N/mm2
4.18 N/mm2
5.36N/mm2
解答 4:最大曲げ応力度は、M / Z で求められる。
M(曲げモーメント) = wl2 / 8 = 6 × 4,0002 / 8 =12,000,000 N・mm
Z(断面係数) = bh2 / 6 = 100 × 2002 / 6 = 4,000,000 / 6 mm3
よって、最大曲げ応力度は、
M / Z = 12,000,000 × 6 / 4,000,000 = 18 N/mm2
〔H28 No.2〕図のような荷重を受ける単純梁に、断面90mm×200mmの部材を用いた場合、A点の断面下端に生じる縁応力度σとして、正しいものは、次のうちどれか。ただし、縁応力度σは下式によって与えられるものとし、部材の断面は一様で、荷重による部材の変形及び自重は無視するものとする。

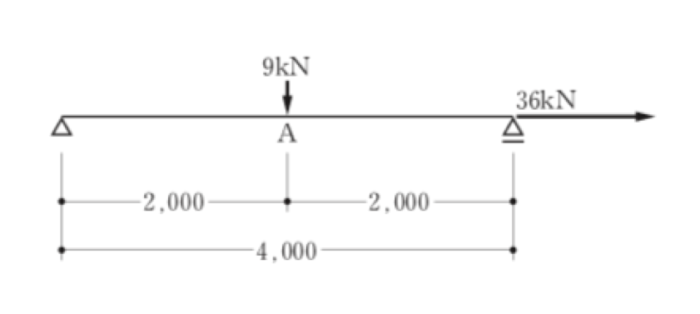
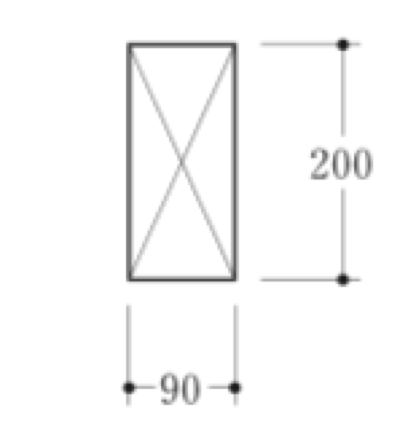

1.13N/mm2
2.17N/mm2
3.22N/mm2
4.32N/mm2
5.35N/mm2
解答 2:
〔H27 No.2〕図のような等分布荷重を受ける単純梁に断面 100mm×300mmの部材を用 いた場合、A点に生じる最大曲げ応力度として、正しいものは、次のうちどれか。ただし、 部材の断面は一様とし、自重は無視するものとする。
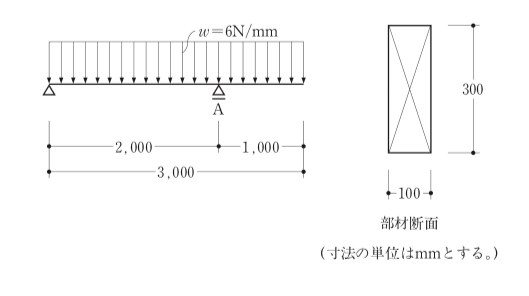
1.1N/mm2
2.2N/mm2
3.3N/mm2
4.4N/mm2
5.5N/mm2
解答 2:
〔H26 No.2〕図のような等分布荷重を受ける単純梁に断面75mm×200mmの部材を用いた場合、A点の最大曲げ応力度が1N/mm2となるときの梁の長さの値として、正しいものは、次のうちどれか。ただし、部材の断面は一様とし、自重は無視するものとする。
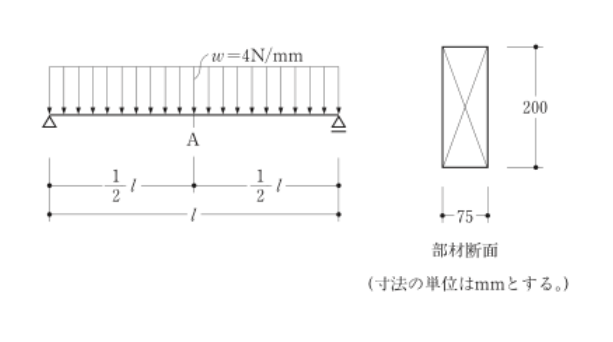
1.1,000mm
2.1,200mm
3.1,500mm
4.1,800mm
5.2,000mm
解答 1:
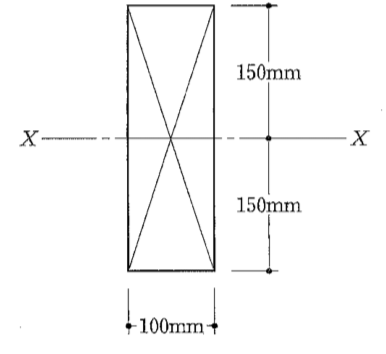
〔H25 No.2〕図のような長方形断面を有する木造の梁のX軸についての許容曲げモーメントとして、正しいものは、次のうちどれか。ただし、梁材の許容曲げ応力度は、12N/mm2とする。
1.6kN・m
2.9kN・m
3.12kN・m
4.18kN・m
5.27kN・m
解答 4:X軸についての許容曲げモーメントMaは、次式から求める。
Z = bh2/6 = 100 × 3002/6 = 1,500,000mm3
fb = 12 N/mm2 より、
Ma = 1,500,000 × 12 = 18,000,000 N・mm = 18 kN・m
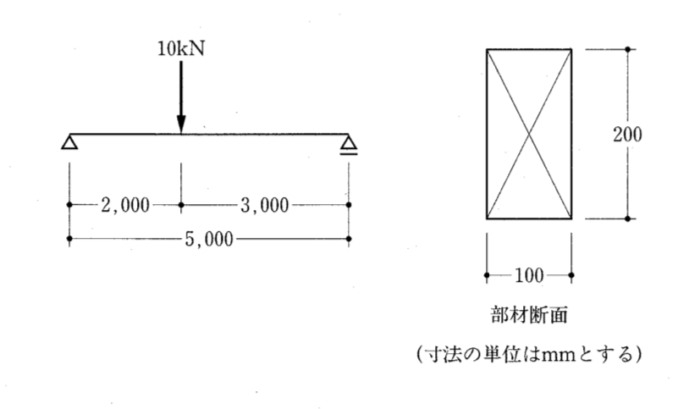
〔H24 No.2〕図のような荷重を受ける単純梁に断面100mm×200mmの部材を用いた場合、その部材に生じる最大曲げ応力度として、正しいものは、次のうちどれか。ただし、部材の自重は無視するものとする。
1.12 N/mm2
2.18 N/mm2
3.24 N/mm2
4.30 N/mm2
5.36 N/mm2
解答 2:最大曲げ応力度は、M / Z で求められる。
曲げモーメントはC点で最大になる。A点における鉛直反力をRAとすると、
M(曲げモーメント) = RA × 2,000 = 6 × 2,000 = 12,000 kN・mm = 12,000,000 N・mm
Z(断面係数) = bh2 / 6 = 100 × 2002 / 6 = 4,000,000 / 6 mm3
よって、最大曲げ応力度は、
M / Z = 12,000,000 × 6 / 4,000,000 = 18 N/mm2
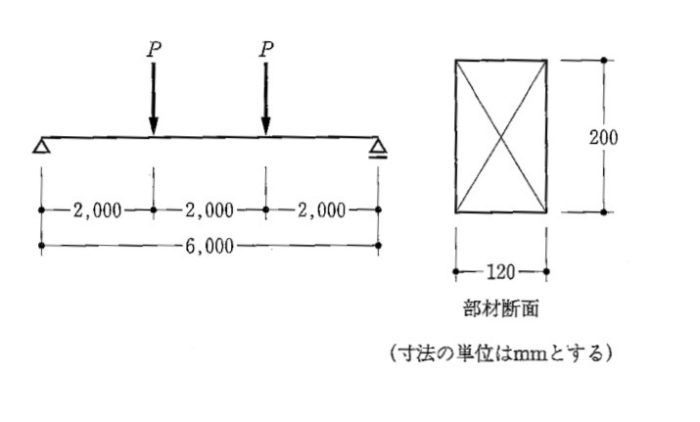
〔H23 No.2〕図のような荷重を受ける単純梁に、断面120mm×200mmの部材を用いた場合、その部材が許容曲げモーメントに達するときの荷重Pの値として、正しいものは、次のうちどれか。ただし、部材の許容曲げ応力度は20N/mm2とし、自重は無視するものとする。
1.4 kN
2.6 kN
3.8 kN
4.12 kN
5.36 kN
解答 3:
〔H21 No.3〕図のような荷重を受ける単純梁に、断面60mm×100mmの部材を用いた場合、その部材に生じる最大曲げ応力度の大きさと最大せん断応力度の大きさとの組合せとして、正しいものは、次のうちどれか。ただし、部材の自重は無視するものとする。
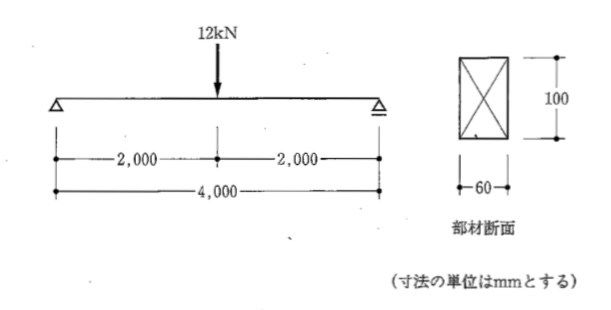
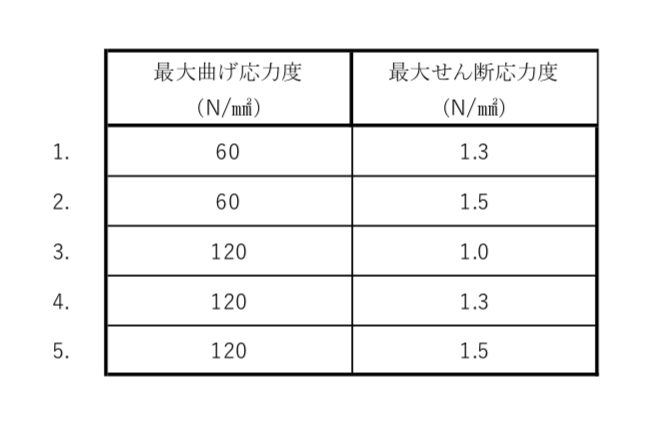
解答 5:最大曲げ応力度は、MMAX / Z 、
最大せん断応力度は、1.5 × QMAX / A で求められる。
曲げモーメントは中心で最大になるので、
MMAX = 6 × 2,000 = 12,000 kN・mm = 12,000,000 N・mm
Z(断面係数) = bh2 / 6 = 60 × 1002 / 6 = 100,000 mm3
よって、最大曲げ応力度は、
M / Z = 12,000,000 / 100,000 = 120 N/mm2
最大せん断力QMAX は 6,000 N、断面積Aは 6,000 mm2。
よって、最大せん断応力度は、
1.5 × QMAX / A = 1.5 × 6,000 / 6,000 = 1.5 N/mm2
〔H20 No.3〕図のような荷重を受ける、スパンが等しく断面の異なる単純梁A及び単純梁Bにおいて、CA点、CB点に生じる最大曲げ応力度をそれぞれσA、σBとしたとき、それらの比σA:σBとして、正しいものは、次のうちどれか。ただし、単純梁に用いる部材はいずれも同じ材質とし、自重は無視するものとする。
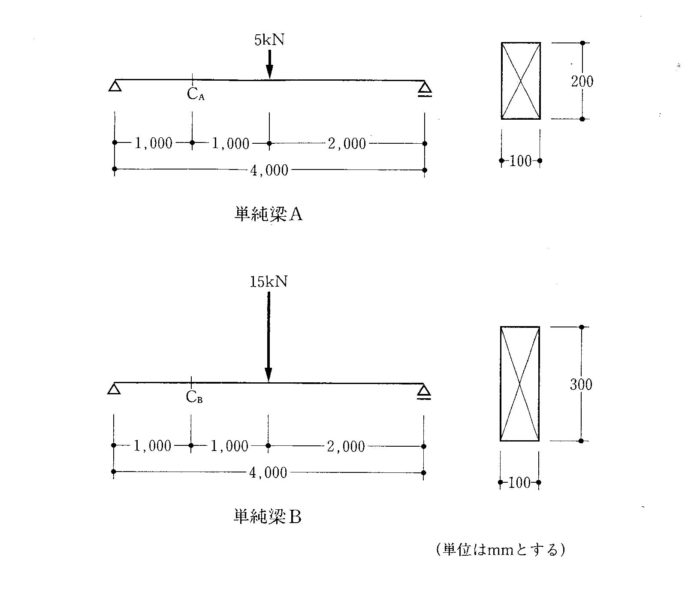
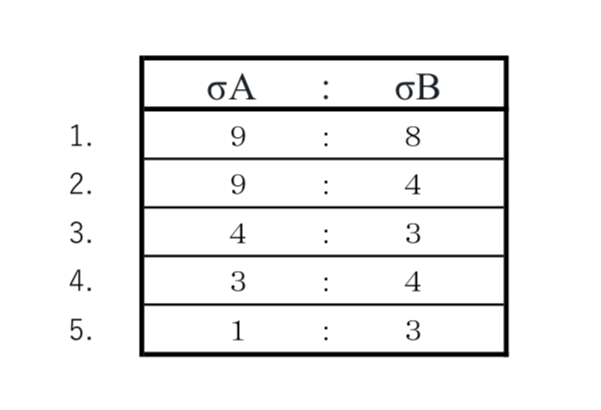
解答 4:曲げ応力度は、σ = M / Z で求められる。
まず、それぞれの梁のMMAXは、
MA・MAX = 2.5 × 2,000 = 5,000 kN・mm
MB・MAX = 7.5 × 2,000 = 15,000 kN・mm
であるから、それぞれMCA、MCBは、
MCA = 2,500 kN・mm
MCB = 7,500 kN・mm
次にそれぞれの断面係数ZA、ZBは、
ZA = bhA2 / 6 = 100 × 2002 / 6 = 4,000,000 / 6 mm3
ZB = bhB2 / 6 = 100 × 3002 / 6 = 9,000,000 / 6 mm3
以上より、σAおよびσBが求められる。
σA = 2,500 × 6 / 4,000,000
σB = 7.500 × 6 / 9,000,000
これら1つを比で表すと、
σA : σA = 1 / 4 : 1 / 3 = 3 : 4
お問い合わせ
※当サイトに関する質問や、当サイトで閲覧した試験問題に関するお問い合わせはこちらまでお願いします。当サイトは公益財団法人建築技術教育普及センターより正式に許諾を得て掲載しております。そのためご利用者様には厳正なご利用をお願しており、当サイトに関する一切のお問い合わせはサイト運営責任者までお願いします(掲載許諾条件(6))。センターへのお問い合わせはご遠慮ください。
おすすめ参考書
過去問題を解くのがやはり合格への近道です
このサイトだけでも学習は可能ですが、紙媒体での学習も不可欠です
解説集は何種類もありますが、管理人のおすすめは以下の書籍!コスパとクオリティの面では…
1級建築士: 「1級建築士分野別厳選問題500+125(2019年度版) [ 日建学院教材研究会 ]」
2級建築士: 「2級建築士分野別厳選問題500+100(2019年度版) [ 日建学院教材研究会 ]」



![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/17b1be22.993548c3.17b1be23.daec8f4f/?me_id=1213310&item_id=19382847&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F5942%2F9784863585942.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F5942%2F9784863585942.jpg%3F_ex%3D240x240&s=240x240&t=picttext)