1級建築士試験H20年学科3No.11
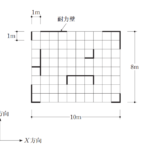
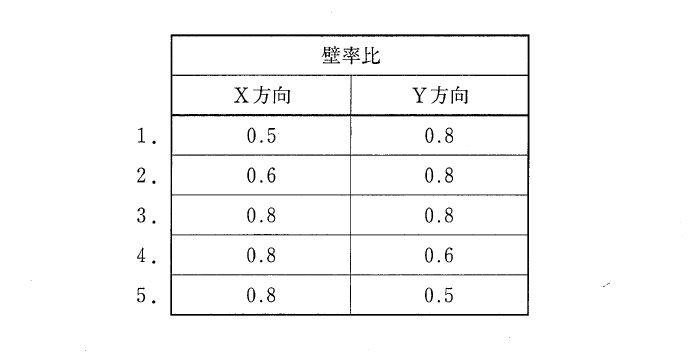
設問:図のような木造の在来軸組工法による平家建ての建築物(屋根は日本瓦葺とする。)において、建築基準法に基づく「木造建築物の軸組の設置の基準」による壁率比の組合せとして、最も適当なものは、次のうちどれか。ただし、図中の太線は耐力壁を示し、その倍率(壁倍率)は1とする。なお、壁率比は、壁量充足率の小さいほうを壁量充足率の大きいほうで除した数値である。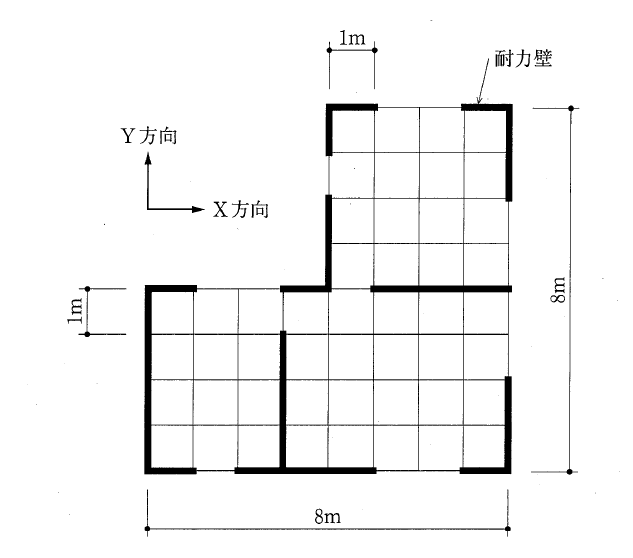
解説
計算手順
木造建築物の軸組の設置の基準(平成12年告示第1352号)に則り、方向別に4分割して壁量充足率を求める。その後に壁率比を求めていく。
・各側端部分の「存在壁量」の計算(令46条4項表1の数値×壁の長さ)
・各側端部分の「必要壁量」の計算(令46条4項表2の数値×点線部分の面積)
・壁量充足率を求める(= 存在壁量/必要壁量)
・壁率比を求める(= 壁量充足率の小さい方/大きい方)
まずX方向の壁量充足率と壁率比を求める。
Y方向の壁の長さが8mなので、その側端部分は、8m×1/4=2mとなり、X軸方向では下図に赤点線で囲む。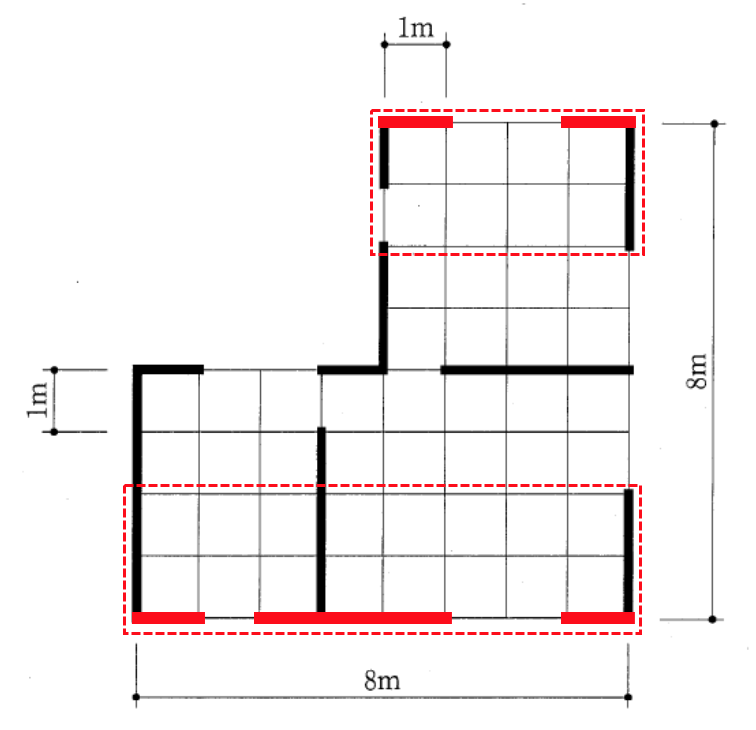
この範囲の中で、X方向の壁量充足率を求める。
まず、存在壁量は令46条4項表1の数値(題意より1)に壁の長さを乗じたもの。必要壁量は令46条4項表2の数値(ここではAとする)に点線部分の面積を乗じて求める。
X = 存在壁量 / 必要壁量
X上 = 2m×1 / A × (2m×4m) = 0.25/A
X下 = 5m×1 / A × (2m×8m) ≒ 0.31/A
次に上で求めた壁量充足率から、壁率比を求める。
壁率比 = 壁量充足率の小さい方/大きい方
= X上 / X下
= 0.25 / 0.31
≒ 0.80
Y方向の壁量充足率と壁率比を求める。
X方向と同様に、X方向はの壁の長さが8mなので、その側端部分は、8m×1/4=2mとなり、Y軸方向では下図に青点線で囲む。
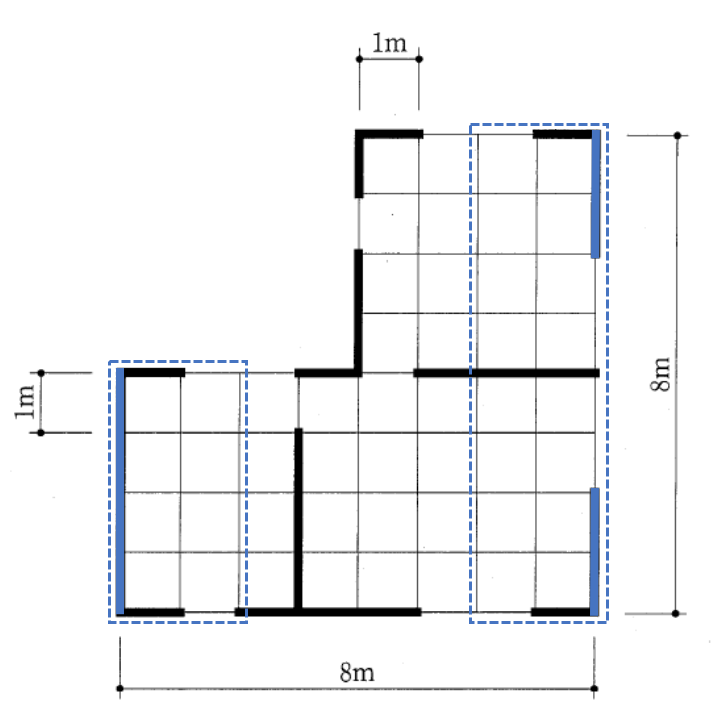
この範囲の中で、X方向と同様にY方向の壁量充足率を求める。
Y右 = 4m×1 / A × (2m×8m) = 0.25/A
Y左 = 4m×1 / A × (2m×4m) = 0.50/A
次に上で求めた壁量充足率から、壁率比を求める。
壁率比 = 壁量充足率の小さい方/大きい方
= Y右 / Y左
= 0.25 / 0.50
= 0.5
よって、壁率比はX方向は0.8、Y方向は0.5である。(選択肢5)
類似問題
平成30年1級学科4、No.10
平成29年1級学科4、No.10
平成27年1級学科4、No.10
平成26年1級学科4、No.09
平成24年1級学科4、No.09
平成23年1級学科4、No.09
平成21年1級学科4、No.10
平成20年1級学科4、No.11
平成30年2級学科3、No.12
平成29年2級学科3、No.11
平成26年2級学科3、No.11
平成24年2級学科3、No.11