二級建築士試験分野別まとめ
構造
変形と不静定構造物

2023年7月02日(日)
令和05年度試験日まであと 日!
このWEBサイトは建築士試験に限定した資料集です
(公益財団法人よりWEB上での公開認定取得済)
分野別にまとめました
(平成20年度から令和02年度まで)
二級建築士
構造
変形と不静定構造物
〔R02 No.6〕図のような長さl(m)の柱(材端条件は、一端自由、他端固定とする。)に圧縮力Pが作用したとき、次のlとIとの組合せのうち、弾性座屈荷重が最も大きくなるものはどれか。ただし、Iは断面二次モーメントの最小値とし、それぞれの柱は同一の材質で、断面は一様とする。
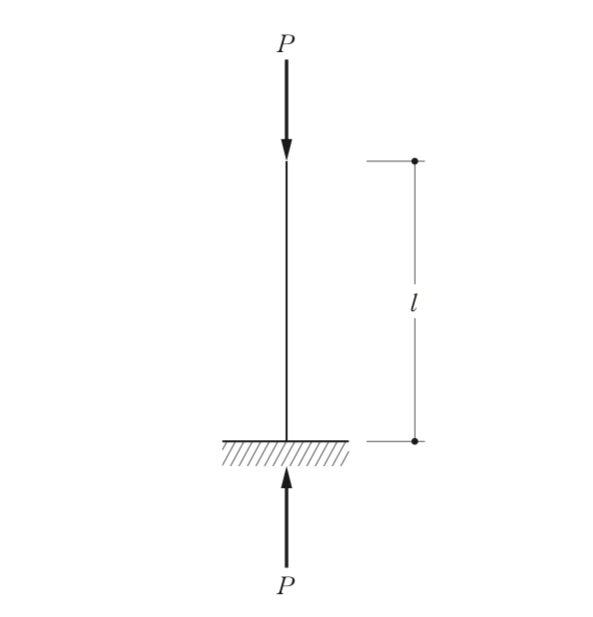
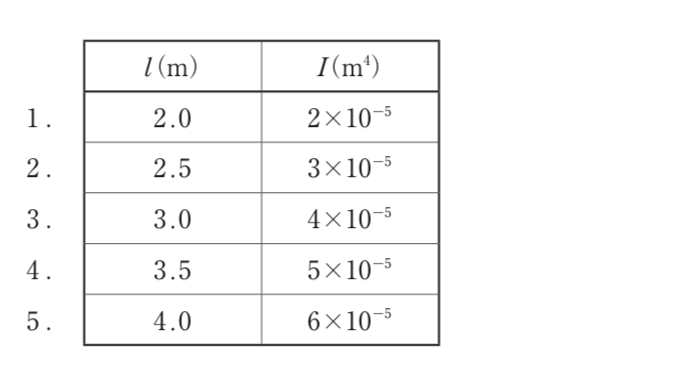
解答 1:弾性座屈荷重(Pe)は、以下の式で求められる。
(E:ヤング係数、I:断面二次モーメント、lk:座屈長さ)
 lk=2l、π2Eは一定、これより、 Pe=I/2l2で比較する。
lk=2l、π2Eは一定、これより、 Pe=I/2l2で比較する。
枝1:(2×10-5)/(2×2.0)2=0.125×10-5
枝2:(3×10-5)/(2×2.5)2=0.120×10-5
枝3:(4×10-5)/(2×3.0)2=0.111×10-5
枝4:(5×10-5)/(2×3.5)2=0.102×10-5
枝5:(6×10-5)/(2×4.0)2=0.094×10-5
よって、弾性座屈荷重は枝1が最も大きくなる。
〔R01 No.6〕図のような材の長さ、材端又は材の中央の支持条件が異なる柱A、B、Cの弾性座屈長さを、それぞれlA、lB、lCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。
〔H30 No.6〕図のような材の長さ及び材端の支持条件が異なる柱A、B、Cの弾性座屈荷重をそれぞれPA 、PB 、PCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。ただし、全ての柱の材質及び断面形状は同じものとする。
1.PA >PB >PC
2.PA =PC >PB
3.PB >PA =PC
4.PC >PA >PB
5.PC >PA >PB
〔H29 No.6〕図のような材の長さ及び材端の支持条件が異なる柱A、B、Cの座屈長さをそれぞれlA、lB、lCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。
1.lA > lC> lB
2.lA = lC> lB
3.lB >lA = lC
4.lB >lC > lA
5.lC> lB>lA
〔H28 No.6〕図のような材の長さ及び材端の支持条件が異なる柱A、B、Cの弾性座屈荷重をそれぞれPA、PB、PCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。ただし、全ての柱の材質及び断面形状は同じものとする。
1.PA > PB > PC
2.PA > PC > PB
3.PA = PB > PC
4.PB > PA >PC
5.PC> PA = PB
〔H27 No.6〕図のような材の長さ及び材端の支持条件が異なる柱A、B、Cの座屈長さを それぞれLA、LB、LCとしたとき、それらの大小関係として、正しいものは、次のうちどれ か。
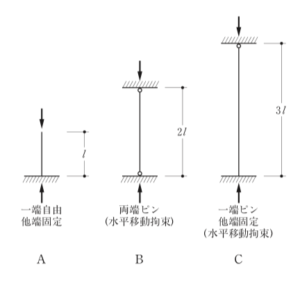
1.LA > LB >LC
2.LA = LB > LC
3.LB > LC > LA
4.LC > LA = LB
5.LC > LB > LA
解答 4:座屈長さ(Lk)は、以下の表から求められる。
 題意より、lA=1.0l、lB=2.0l、lC=3.0l、
題意より、lA=1.0l、lB=2.0l、lC=3.0l、
LkA=2.0LA=2.0×1.0l=2.0l
LkB=1.0LB=1.0×2.0l=2.0l
LkC=0.7LC=0.7×3.0l=2.1l
よって座屈長さ(Lk)は、LkC > LkA =LkB となる。
〔H24 No.4〕図のような長さl(m)の柱(材端条件は、一端自由、他端固定とする。)に圧縮力Pが作用したとき、次のlとI との組合わせのうち、弾性座屈荷重が最も大きくなるものはどれか。ただし、Iは断面二次モーメントの最小値とし、それぞれの柱は同一の材質で、断面は一様とする。
解答 2:弾性座屈荷重(Pe)は、以下の式で求められる。
〔H23 No.7〕図のような材の長さ及び材端の支持条件が異なる柱A、B、Cの弾性座屈荷重をそれぞれPA、PB、PCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。ただし、すべての柱の材質及び断面形状は同じものとする。

1.PA > PB > PC
2.PA > PC > PB
3.PB > PA > PC
4.PB > PA = PC
5.PC > PA > PB
解答 3:弾性座屈荷重(P)は、以下の式で求められる。
(E:ヤング係数、I:断面二次モーメント、lk:座屈長さ)
 題意より、LA=3l、LB=2l、LC=0.9l、
題意より、LA=3l、LB=2l、LC=0.9l、
lkA=0.5LA、lkB=0.7LB、lkC=2.0LC
π2EIは一定なので、 P=1/lk2で比較する。
PA=1/(0.5×3l)2=1/(1.5l)2
PB=1/(0.7×2l)2=1/(1.4l)2
PC=1/(2.0×0.9l)2=1/(1.8l)2
よって、弾性座屈荷重はPB > PA > PCとなる。
〔H22 No.7〕図のような長さl(m)の柱(材端条件は、両単品、水平移動拘束とする。)に圧縮力Pが作用したとき、次のlとIとの組合せのうち、弾性座屈荷重が最も大きくなるものはどれか。ただし、Iが断面二次モーメントの最小値とし、それぞれの柱は同一の材質で、断面は一様とする。
解答 5:
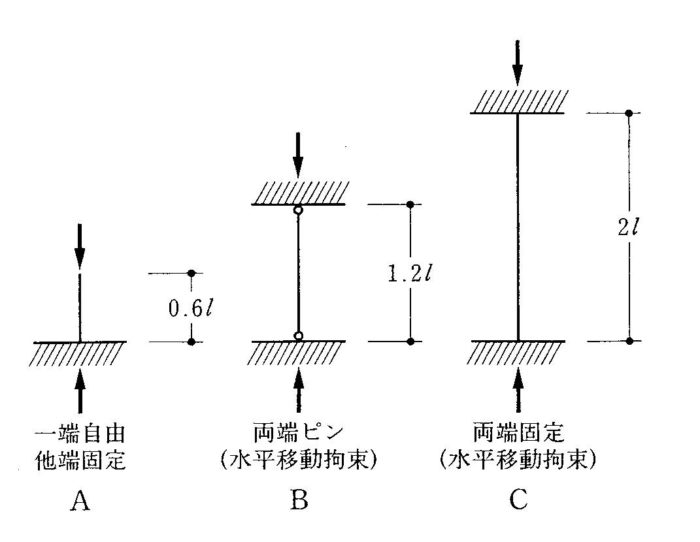
〔H20 No.5〕図のような材の長さ及び材端の支持条件が異なる柱A、B、Cの弾性座屈荷重をそれぞれPA、PB、PCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。ただし、すべての柱の材質及び断面形状は同じものとする。
1.PC>PA=PB
2.PB>PA=PC
3.PB>PC>PA
4.PA>PB>PC
5.PA=PC>PB
解答 1:弾性座屈荷重(P)は、以下の式で求められる。
(E:ヤング係数、I:断面二次モーメント、lk:座屈長さ)
 題意より、LA=0.6l、LB=1.2l、LC=2.0l、
題意より、LA=0.6l、LB=1.2l、LC=2.0l、
lkA=2.0LA、lkB=1.0LB、lkC=0.5LC
π2EIは一定なので、 P=1/lk2で比較する。
PA=1/(2.0×0.6l)2=1/(1.2l)2
PB=1/(1.0×1.2l)2=1/(1.2l)2
PC=1/(0.5×2.0l)2=1/(1.0l)2
よって、弾性座屈荷重はPC>PA=PB となる。
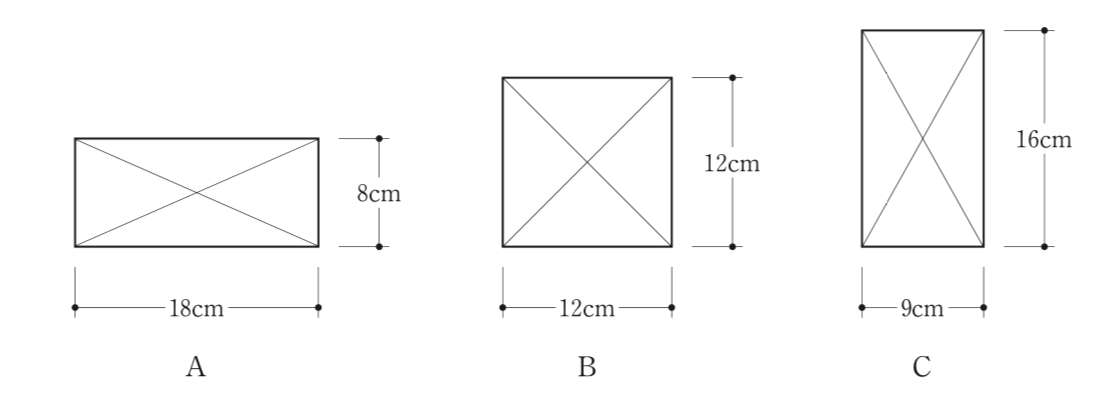
〔H26 No.6〕図のような断面を有する長柱A、B、Cの弾性座屈荷重をそれぞれPA、PB、PCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。ただし、全 ての柱の材質は同じで、座屈長さは等しいものとする。
1.PA < PB < PC
2.PB < PA < PC
3.PB < PC < PA
4.PC < PA < PB
5.PC < PB < PA
解答 3:弾性座屈荷重(Pe)は、以下の式で求められる。
(E:ヤング係数、I:断面二次モーメント、lk:座屈長さ)
また長方形の断面二次モーメント(I)は、以下の式で求められる。
以上2式をまとめると、
題意より「π2E /12lk2」は一定なので、bh3で比較する。
長柱A:18cm×8cm3=9,216cm4
長柱B:12cm×12cm3=20,736cm4
長柱C:16cm×9cm3=11,664cm4
よって、PB < PC < PAとなる。
〔H25 No.6〕長柱の弾性座屈荷重に関する次の記述のうち、最も不適当なものはどれか。
1.弾性座屈荷重は、材料のヤング係数に比例する。
2.弾性座屈荷重は、柱の断面二次モーメントに比例する。
3.弾性座屈荷重は、柱の曲げ剛性に反比例する。
4.弾性座屈荷重は、柱の座屈長さの2乗に反比例する。
5.弾性座屈荷重は、柱の両端の支持条件がピンの場合より固定の場合のほうが大きい。
解答 3:弾性座屈荷重(Pe)は、以下の式で求められる。
(E:ヤング係数、I:断面二次モーメント、lk:座屈長さ)
よって、弾性座屈荷重は、曲げ剛性(EI)に比例する。
〔H21 No.7〕長柱の弾性座屈荷重に関する次の記述のうち、最も不適当なものはどれか。
1.弾性座屈荷重は、材料のヤング係数に反比例する。
2.弾性座屈荷重は、柱の座屈長さの2乗に反比例する。
3.弾性座屈荷重は、柱の断面二次モーメントに比例する。
4.弾性座屈荷重は、柱の両端の支持条件が「水平移動自由で両端固定の場合」と「水平移動拘束で両端ピンの場合」とでは、同じとなる。
5.弾性座屈荷重は、柱の両端の支持条件がピンの場合より固定の場合のほうが大きい。
解答 1:弾性座屈荷重(Pe)は、以下の式で求められる。
(E:ヤング係数、I:断面二次モーメント、lk:座屈長さ)
よって、弾性座屈荷重は、材料のヤング係数(E)に反比例する。
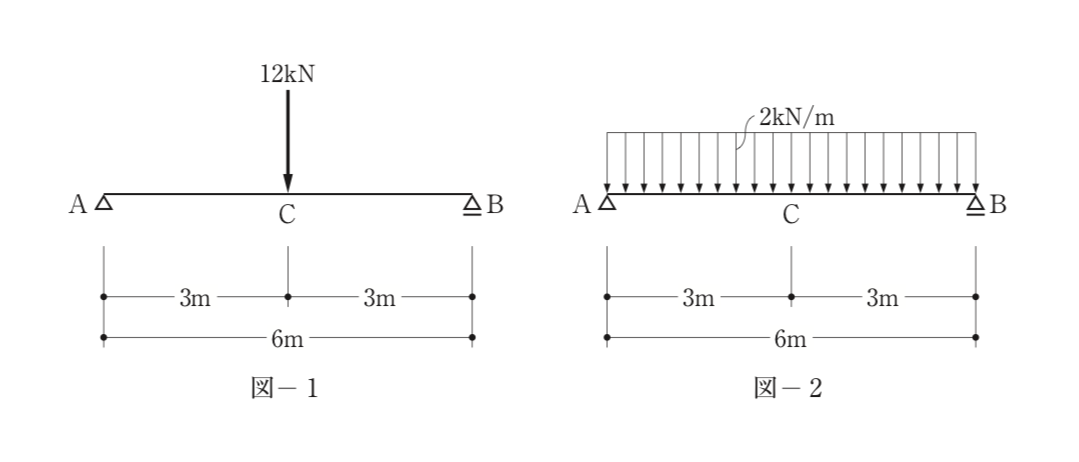
〔R02 No.3〕図-1のように集中荷重を受ける単純梁を、図-2のような等分布荷重を受けるように荷重条件のみ変更した場合に生じる変化に関する次の記述のうち、最も不適当なものはどれか。ただし、梁は自重を無視するものとする。
1.支点A及びBの反力は、荷重条件変更後も、変わらない。
2.最大曲げモーメントが、荷重条件変更後に、小さくなる。
3.C点におけるたわみが、荷重条件変更後に、小さくなる。
4.軸方向力は、荷重条件変更後も、変わらない。
5.最大せん断力が、荷重条件変更後に、小さくなる。
解答 5:それぞれの最大せん断力をQ1max、Q2maxとすると、
Q1max=6kN(梁ABに一様に6kNのせん断力が生じる)
Q2max=9kN(梁の中心点Cに最大せん断力が生じる)
よって、最大せん断力は荷重条件変更後に大きくなる。
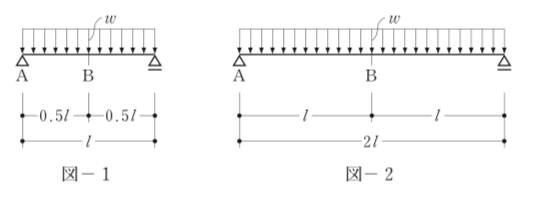
〔H25 No.5〕図-1のような単純梁を図-2のように、等分布荷重w(N/m)を変えずに、スパンl(m)を2倍にした場合に生じる変化に関する次の記述のうち、最も不適当なものはどれか。ただし、梁は、自重を無視するものとし、材質及び断面は変わらないものとする。
1.A点のたわみ角が4倍になる。
2.B点のたわみが16倍になる。
3.A点の鉛直反力が2倍になる。
4.最大せん断力が2倍になる。
5.最大曲げモーメントが4倍になる。
解答 1:図-1のたわみ角(θA1)は、(1/24)・Wl2/EIである。W=wlより、
θA1 = (1/24)・Wl2/EI = (1/24)・wl3/EI
図-2のたわみ角(θA2 )はθA1 のスパンの2倍なので、
θA2 =(1/24)・w(2l)3/EI = 8・ {(1/24)・Wl2/EI} = 8θA1
よって、A点のたわみ角は8倍になる。
〔H20 No.4〕図-1のような単純梁を図-2のように、等分布荷重w(kN/m)を変えずに、スパンl(m)を2倍にした場合に生じる変化に関する次の記述のうち、最も不適当なものはどれか。ただし、梁は、自重を無視するものとし、材質及び断面は変わらないものとする。
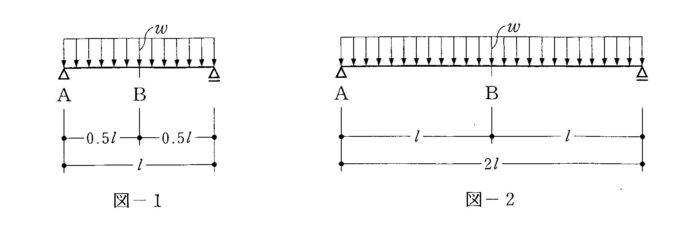
1.A点のたわみ角が8倍になる。
2.B点のたわみが16倍になる。
3.A点の鉛直反力が2倍になる。
4.最大せん断力が2倍になる。
5.最大曲げモーメントが2倍になる。
解答 5:図-1の最大曲げモーメント(M1)は、Wl / 8である。W=wlより、
M1 = Wl / 8 = wl2/ 8
図-2の最大曲げモーメント(M2 )はM1 のスパンの2倍なので、
M2 =w(2l)2 / 8 = 4 {wl2/ 8} = 4M1
よって、最大曲げモーメントは4倍になる。
お問い合わせ
※当サイトに関する質問や、当サイトで閲覧した試験問題に関するお問い合わせはこちらまでお願いします。当サイトは公益財団法人建築技術教育普及センターより正式に許諾を得て掲載しております。そのためご利用者様には厳正なご利用をお願しており、当サイトに関する一切のお問い合わせはサイト運営責任者までお願いします(掲載許諾条件(6))。センターへのお問い合わせはご遠慮ください。
おすすめ参考書
過去問題を解くのがやはり合格への近道です
このサイトだけでも学習は可能ですが、紙媒体での学習も不可欠です
解説集は何種類もありますが、管理人のおすすめは以下の書籍!コスパとクオリティの面では…